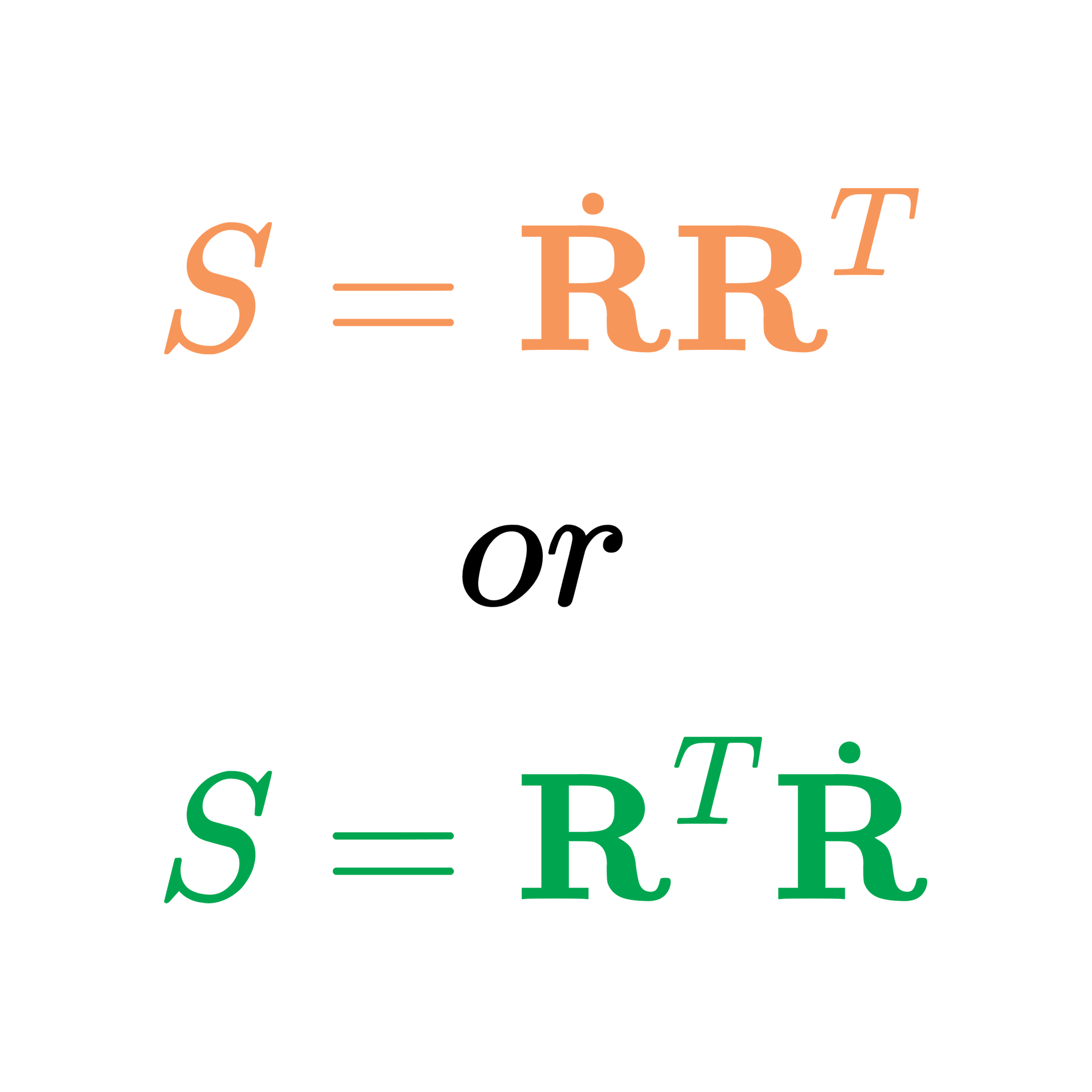什么是齐次变换矩阵

空间描述

为了描述一个刚体在空间中的运动，我们需要表达出它的位置和姿态。

位置

在坐标系 $\left \{A \right \}$ 中，任意点可以表示成一个 $3 \times 1$ 的位置矢量

$$
\sideset{^A}{}P = \begin{bmatrix}
p_x \\
p_y \\
p_z
\end{bmatrix}
$$

姿态

设 $\left \{B \right \}$ 为刚体的固连系，刚体的姿态定义为 $\left \{B \right \}$ 的三个基矢量 $\hat{X} _B, \hat{Y} _B, \hat{Z} _B$ 在 $\left \{A \right \}$ 中的坐标，将这三个坐标拼成一个矩阵，

$$
\begin{align*}
\sideset{_B^A}{}R &= \begin{bmatrix}
\sideset{^A}{}{\hat X}_B &\sideset{^A}{}{\hat Y}_B &\sideset{^A}{}{\hat Z}_B
\end{bmatrix} \\
&= \begin{bmatrix}
{\hat X}_B \cdot {\hat X}_A &{\hat Y}_B \cdot {\hat X}_A &{\hat Z}_B \cdot {\hat X}_A \\
{\hat X}_B \cdot {\hat Y}_A &{\hat Y}_B \cdot {\hat Y}_A &{\hat Z}_B \cdot {\hat Y}_A \\
{\hat X}_B \cdot {\hat Z}_A &{\hat Y}_B \cdot {\hat Z}_A &{\hat Z}_B \cdot {\hat Z}_A
\end{bmatrix}
\end{align*}
$$

这样的 $\sideset{_B^A}{}R$ 是一个旋转矩阵（行列式为1的正交矩阵）。

位姿

$\left \{B \right \}$ 在 $\left \{A \right \}$ 中的位姿可以用 $\left \{B \right \}$ 原点的位置矢量 $\sideset{^A}{ _{BORG}}P$ 和一个旋转矩阵 $\sideset{_B^A}{}R$ 描述

$$
\left \{B \right \} = \begin{Bmatrix} \sideset{_B^A}{}R &\sideset{^A}{ _{BORG}}P \end{Bmatrix}
$$

坐标变换

空间中一个点在不同坐标系中有不同的坐标，坐标之间的变换关系取决于坐标系的相对关系。

平移

若 $\left \{A \right \}$ 与 $\left \{B \right \}$ 的姿态相同，对于空间中任意一点，有

$$
\sideset{^A}{}P = \sideset{^B}{}P + \sideset{^A}{ _{BORG}}P
$$

旋转

若 $\left \{A \right \}$ 与 $\left \{B \right \}$ 的原点相同，对于空间中任意一点，有

$$
\sideset{^A}{}P = \sideset{ _B^A}{}R \sideset{^B}{}P
$$

一般变换

$\left \{B \right \}$ 的原点在 $\left \{A \right \}$ 中的坐标为 $\sideset{^A}{ _{BORG}}P$ ，同时 $\left \{B \right \}$ 相对 $\left \{A \right \}$ 的旋转矩阵为 $\sideset{_B^A}{}R$ ，则有

$$
\sideset{^A}{}P = \sideset{ _B^A}{}R \sideset{^B}{}P + \sideset{^A}{ _{BORG}}P \tag{*}
$$

为了书写的简洁，定义一个 $4 \times 4$ 矩阵

$$
\sideset{_B^A}{}T = \begin{bmatrix}
\sideset{ _B^A}{}R &\sideset{^A}{ _{BORG}}P \\
0 &1
\end{bmatrix}
$$

则(*)可改写为

$$
\begin{bmatrix}
\sideset{^A}{}P \\ 1
\end{bmatrix} = \sideset{_B^A}{}T \begin{bmatrix}
\sideset{^B}{}P \\ 1
\end{bmatrix}
$$

进一步，用 $\sideset{^A}{}P$ 和 $\sideset{^B}{}P$ 代替 $\begin{bmatrix}\sideset{^A}{}P \\ 1\end{bmatrix}$ 和 $\begin{bmatrix}\sideset{^B}{}P \\ 1\end{bmatrix}$ ，于是(*)化为

$$
\sideset{^A}{}P = \sideset{ _B^A}{}T \sideset{^B}{}P
$$

$\sideset{ _B^A}{}T$ 称为 $\left \{B \right \}$ 相对于 $\left \{A \right \}$ 的齐次变换矩阵，它能够完整描述一个坐标系的位姿，可以将坐标变换表示成线性变换。

齐次变换矩阵的应用

在Minecraft中的应用

Minecraft JAVA 1.19.4 中加入了展示实体，包括物品展示实体、方块展示实体和文本展示实体（以下的演示皆用方块展示实体）。展示实体要展示出来，就必须确定实体的位置和姿态（利用transformation标签）。游戏内提供了多种表示位姿的方式，如矩阵形式、轴-角度旋转、四元数旋转以及缩放等，其中矩阵形式指的就是齐次变换矩阵或者它的变体。

在不添加transformation标签的情况下，方块展示实体为默认状态。例如

1	summon minecraft:block_display ~0.5 ~0.5 ~0.5 {block_state:{Name:"minecraft:diamond_block"}}

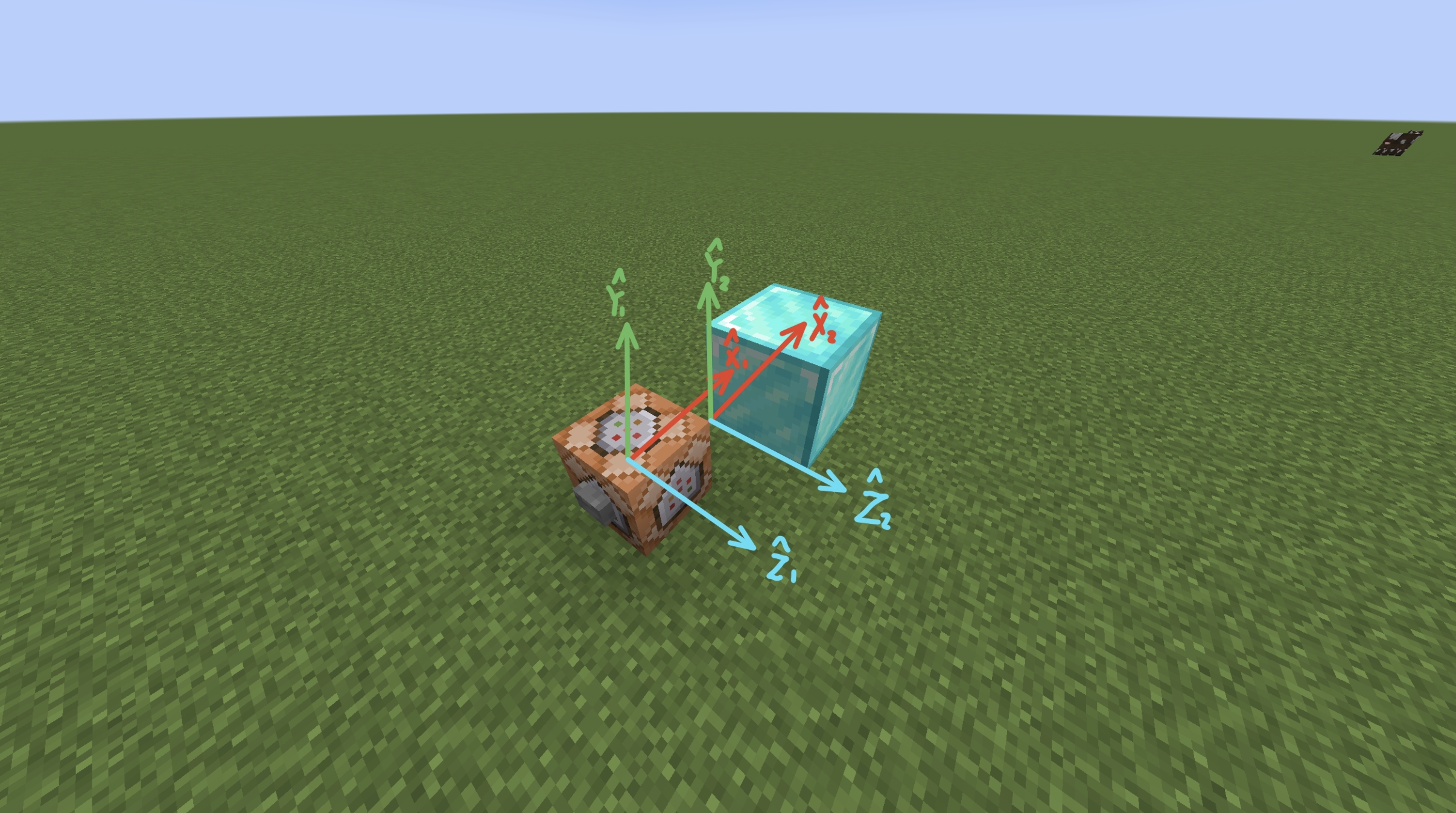
我在图中建立了两个参考系 $\left \{1 \right \}$ 和 $\left \{2 \right \}$ 。其中 $\left \{1 \right \}$ 的原点在命令方块的中心，三个轴的指向是与游戏内一致的，x轴指向东，y轴竖直向上，z轴指向南。$\left \{2 \right \}$ 的姿态与 $\left \{1 \right \}$ 完全相同，但 $\left \{2 \right \}$ 的原点相对 $\left \{1 \right \}$ 有一个偏离，这由命令中的’~0.5 ~0.5 ~0.5’决定，写成位置表达式：

$$
\sideset{^1}{_2}P = \begin{bmatrix}
0.5 \\ 0.5 \\ 0.5
\end{bmatrix}
$$

于是我们可以通过简单地设置summon的召唤位置来控制展示实体的位置，但这样难以改变它的姿态。

为了同时改变展示实体的位置和姿态，可以在命令中添加transformation标签，然后按行优先的方式输入一个齐次变换矩阵。例如

summon minecraft:block_display ~0.5 ~0.5 ~0.5 {
block_state:{Name:"minecraft:diamond_block"},
transformation:
[0.6f,0.8f,0f,1f,
-0.8f,0.6f,0f,1f,
0f,0f,1f,0f,
0f,0f,0f,1f]
}

加入transformation标签后，实体固连系就不再与 $\left \{2 \right \}$ 重合，我们将其称为 $\left \{3 \right \}$ 系。$\left \{2 \right \}$ 与 $\left \{3 \right \}$ 的关系体现为指令中的齐次变换矩阵：

$$
\sideset{_3^2}{}T = \begin{bmatrix}
0.6 &0.8 &0 &1 \\
-0.8 &0.6 &0 &1 \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{bmatrix}
$$

分开来看，

$$
\sideset{_3^2}{}R = \begin{bmatrix}
0.6 &0.8 &0 \\
-0.8 &0.6 &0 \\
0 &0 &1
\end{bmatrix}
\sideset{^2}{_3}P = \begin{bmatrix}
1 \\ 1 \\ 0
\end{bmatrix}
$$

意味着 $\left \{3 \right \}$ 是 $\left \{2 \right \}$ 沿 $\hat{X} _2$ 方向平移1个单位，沿 $\hat{Y} _2$ 方向平移1个单位，绕着 $\hat{Z} _2$ 轴顺时针旋转53.13°的结果。

另外，指令中填写的矩阵不一定非得是标准的齐次变换矩阵。如果左上角 $3 \times 3$ 旋转矩阵部分的行列式不为1，会产生缩放效果，行列式小于0，会出现内外翻转现象（ $\left \{3 \right \}$ 变成了左手系）。如果矩阵(4,4)的位置不是1，则游戏会自动对矩阵进行整体缩放，使得 $T_{4,4}=1$ 。