注：完整代码在 https://github.com/GreenZhu233/quadrotor-circle-formation.git

实现思路

模型准备：使用gazebo官方的四旋翼无人机模型
控制思路：在无人机模型中添加 gazebo_ros_force 和 gazebo_ros_p3d 插件。通过 gazebo_ros_p3d 读取无人机的位姿、速度、角速度信息，利用 gazebo_ros_force 向无人机传递力和力矩信息，以此来实现闭环控制。
编队算法来自论文： Wang, Xie - 2017 - Limit-cycle-based decoupled design of circle formation control with collision avoidance for anonymous agents in a pla

创建功能包

在工作空间的 /src 目录下使用 ROS2 指令 ros2 pkg create quadrotor_formation --build-type ament_python --dependencies rclpy ，创建一个由python编写的功能包。

无人机模型描述文件

在 Gazebo 默认模型路径中找到 /quadrotor 文件夹，可以看到内部存放一个文件夹和几个文件，重点关注 model.sdf 文件和 /meshes 文件夹。其中 model.sdf 描述的是四旋翼无人机的质量(mass)、惯量矩阵(inertia)、碰撞信息(collision)以及视觉信息(visual)。由于该无人机模型只是一个简单的刚体，因此 sdf 文件中的 link 标签只有一个，没有出现 joint 标签。此外，collision 与 vision 这两个标签共同引用了 /meshes 文件夹下的 quadrotor_base.dae，这个文件存储着整个四旋翼无人机的建模。

model.sdf

<?xml version="1.0" ?>
<sdf version="1.5">
  <model name="quadrotor">
    <link name="link">
      <pose>0 0 0.182466 0 0 0</pose>
      <inertial>
        <mass>1.316</mass>
        <inertia>
          <ixx>0.0128</ixx>
          <ixy>0</ixy>
          <ixz>0</ixz>
          <iyy>0.0128</iyy>
          <iyz>0</iyz>
          <izz>0.0218</izz>
        </inertia>
      </inertial>
      <collision name="collision">
        <geometry>
          <mesh>
            <uri>model://quadrotor/meshes/quadrotor_base.dae</uri>
          </mesh>
        </geometry>
      </collision>
      <visual name="visual">
        <geometry>
          <mesh>
            <uri>model://quadrotor/meshes/quadrotor_base.dae</uri>
          </mesh>
        </geometry>
      </visual>
    </link>
  </model>
</sdf>

为了给模型添加 gazebo 插件，在其自带的的描述文件 model.sdf 中修改并不妥。为此，在功能包里添加一个名为 /urdf 的文件夹，在其中新建一个xacro文件：quadrotor.xacro ，将 model.sdf 的内容复制到 quadrotor.xacro 中。但是为了保持与 ROS2 的兼容性，需要在文档中作部分修改：

<?xml version="1.0"?>
<robot name="quadrotor" xmlns:xacro="http://www.ros.org/wiki/xacro">
  <link name="base_link">
    <pose>0 0 0.182466 0 0 0</pose>
    <inertial>
      <mass value="1.316"/>
      <inertia ixx="0.0128" ixy="0" ixz="0" iyy="0.0128" iyz="0" izz="0.0218" />
    </inertial>
    <collision name="collision">
      <geometry>
        <mesh filename="model://quadrotor/meshes/quadrotor_base.dae" />
      </geometry>
    </collision>
    <visual name="visual">
      <geometry>
        <mesh filename="model://quadrotor/meshes/quadrotor_base.dae" />
      </geometry>
    </visual>
  </link>
</robot>

其中的 mesh 路径 model://quadrotor/meshes/quadrotor_base.dae 无需修改，因为 gazebo 识别到前缀 model://quadrotor 时，会自动在其环境变量 $GAZEBO_MODEL_PATH 中寻找 /quadrotor 文件夹，从而读取到所需的无人机 mesh 文件。

接下来是添加两个插件的部分。在 quadrotor.xacro 的 <robot> 中添加一个 <gazebo> 标签，填入两个插件的信息：

<robot>
  <xacro:arg name="namespace" default="quad_0" />
  <link> ... </link>
  <gazebo>
    <plugin name="gazebo_ros_force" filename="libgazebo_ros_force.so">
      <ros>
        <namespace>/$(arg namespace)</namespace>
        <remapping>gazebo_ros_force:=gazebo_ros_force</remapping>
      </ros>
      <link_name>base_link</link_name>
      <force_frame>world</force_frame>
    </plugin>
    <plugin name="robot_pos" filename="libgazebo_ros_p3d.so">
      <ros>
        <namespace>/$(arg namespace)</namespace>
        <remapping>odom:=odom</remapping>
      </ros>
      <body_name>base_link</body_name>
      <frame_name>world</frame_name>
      <update_rate>30</update_rate>
    </plugin>
  </gazebo>
</robot>

由于编队的无人机是多个实体，它们所对应的 ROS2 节点不能共用一个名字，因此在 xacro 中添加一个参数 namespace，为每一无人机设定一个名字空间以进行区分，这样与之相关的话题都会带上名字空间作为前缀。xacro 的特性允许在外部调用该文件时对参数进行赋值。
remapping 用来定义插件发布或订阅的话题名称。力与力矩话题称为 gazebo_ros_force，里程计话题称为 odom。
frame_name 标签决定了传递的信息采用的参考坐标系，这里都采用 world 世界坐标系，能够为后续的计算提供便利性。

无人机起飞和编队的控制代码

在功能包的 /quadrotor_formation 文件夹下创建文件 circle_formation.py，其中包含一个总控节点，通过 ROS2 的话题机制订阅所有无人机的位姿速度(或称为里程计 Odometry)信息(由 gazebo_ros_p3d 插件提供)，同时向所有无人机发布力和力矩信息(由 gazebo_ros_force 插件监听)；得到动力学输入后，gazebo再对所有无人机的运动状态进行仿真计算，从而实现对所有无人机起飞和编队动作的闭环控制。

stateDiagram-v2 circle_formation.py --> libgazebo_ros_force.so : gazebo_ros_force libgazebo_ros_force.so --> gazebo动力学演算 gazebo动力学演算 --> libgazebo_ros_p3d.so libgazebo_ros_p3d.so --> circle_formation.py : odom

多线程订阅里程计话题

由于控制节点中存储的每个无人机的位姿与速度信息需要不断更新（从 gazebo 中获得），因此考虑为 odom 的订阅者放在一个线程中循环执行。
首先为控制节点创建一个回调组，然后为每个无人机创建里程计订阅者，并将所有订阅者放入回调组中，最后创建一个多线程执行器，用以循环执行该回调组。

from rclpy.node import Node
from nav_msgs.msg import Odometry
from rclpy.callback_groups import MutuallyExclusiveCallbackGroup
class SteeringNode(Node):
    self.callback_group = MutuallyExclusiveCallbackGroup()
	for quad in self.quadlist:
		self.create_subscription(
			Odometry,
			f"{quad.namespace}/odom",
			quad.odom_callback,
			10,
			callback_group=self.callback_group)

from rclpy.executors import MultiThreadedExecutor
def main():
    executor = MultiThreadedExecutor()
    executor.add_node(node)
    odom_thread = threading.Thread(target=executor.spin)
    odom_thread.start()

其中 quad.odom_callback 是处理订阅信息的方法，用于将接收的里程计信息存储到无人机的属性中。

起飞阶段

令生成的无人机平稳起飞到达指定高度是进行空中编队的前提。
简单起见，这里采用两段抛物线过渡的方式进行控制，如图所示。假设一架无人机需要在 $\left[0,t _f \right]$ 的时间内，高度从 $h _0$ 变化到 $h _f$。在 $\left[0,\frac{t _f}{2}\right]$ 时间内，它的加速度是 $\frac{4(h _f-h _0)}{t _f^2}$；在 $\left[\frac{t _f}{2}, t _f\right]$ 时间内，它的加速度是 $-\frac{4(h _f-h _0)}{t _f^2}$。将目标加速度与无人机的质量相乘，再补充克服重力，就能够得出起飞阶段需要加在每一个无人机身上的力了。

姿态保持

在无人机起飞过程中，由于失去了地面的支撑力，尽管主动力施加在质心上，无人机也可能因扰动产生期望之外的角速度，因此这里采用一个PD控制器实现对无人机姿态的控制。
将无人机当前的姿态四元数记为 $Q$，期望姿态的四元数记为 $Q _0$，可以定义误差四元数为 $Q _\epsilon=Q _0 \circ Q^{-1}$。PD控制器的比例部分与误差四元数有关，导数部分与角速度有关，公式如下：
$$
\vec{M}=k _p\vec{\epsilon} - k _d\vec{\omega}
$$
其中 $\vec{M}$ 是控制力矩在世界坐标系的分量，$\vec{\epsilon}$ 是误差四元数 $Q _\epsilon$ 虚部对应的三维向量，$\vec\omega$ 是无人机当前的角速度在世界坐标系的分量，$k _p$ 与 $k _d$ 是两个正常数对角矩阵。只要通过合理设置参数值，就能得到较为不错的控制效果。
在起飞阶段，每个无人机只需要保持初始姿态，将目标四元数设为 $1$，利用PD控制器向无人机输入恰当的力矩，就能够保证每个无人机都不会在空中出现自转的现象。

import numpy as np
import quaternion as qt
class Quadrotor:
    def orientation_control(self, desired_quat = np.quaternion(1, 0, 0, 0)):
        kp = np.array(self.inertia) * 2
        kd = np.array(self.inertia) * 10
        error_quat = desired_quat * self.ori.inverse()
        torque = kp * np.array([error_quat.x, error_quat.y, error_quat.z])- kd * np.array([self.wx, self.wy, self.wz])
        return torque

这里选择把 $k _p$ 和 $k _d$ 都设成了惯量矩阵的整数倍。

因为惯量矩阵和这两个参数都是对角阵，在代码中简化为1*3向量，所以第8行的乘法运算用星号表示。

编队算法

在所有无人机起飞到制定高度后，登场的就是环形编队算法了。算法的理论推导和可靠性证明参考论文 Wang, Xie - 2017 - Limit-cycle-based decoupled design of circle formation control with collision avoidance for anonymous agents in a pla。
论文中采用分布式控制方法，对所有无人机逆时针排序后，每个无人机只需要实时更新三个向量信息——无人机与圆心和无人机与相邻两无人机之间的向量，就能够计算出自身此刻应该以怎样的速度运动。当所有无人机都采用相同的算法，就能够保证最终无人机按预定的圆心、半径、角距离实现环形编队，并绕圆心同步公转。

根据这三个向量信息，可以计算出与之相关的两个角距离 $\hat\alpha _{i^-}$ 和 $\hat\alpha _i$。

$$\begin{align*}
\hat\alpha _{i^-} =\arctan \frac{\left[ (\bar{p} _i-\hat{p} _{i^-}) \times \bar{p} _i\right] \cdot \vec{n}}{\left\|\bar{p} _i \cdot (\bar{p} _i-\hat{p} _{i^-})\right\|} \\
\hat\alpha _i =\arctan \frac{\left[\bar{p} _i \times (\bar{p} _i+\hat{p} _{i})\right] \cdot \vec{n}}{\left\|\bar{p} _i \cdot (\bar{p} _i+\hat{p} _{i})\right\|}
\end{align*}
$$
代码中的反正切使用 atan2 函数，得到的角度值域为 $\left[-\pi, \pi \right]$。

当编队完成时，这两个角距离将与目标值 $d _{i^-}$ 和 $d _i$ 相等。

控制算法如下：
$$
u _i(t) = \lambda \begin{bmatrix}
\gamma(r^2-\left \|\bar{p} _i(t) \right \|^2 ) &-1 \\
1 &\gamma(r^2-\left \|\bar{p} _i(t) \right \|^2 )
\end{bmatrix} \bar{p} _i(t) \left \{c _1+\frac{c _2}{2\pi}\left[\frac{d _{i^-}}{d _i+d _{i^-}}\hat\alpha _i(t)-\frac{d _i}{d _i+d _{i^-}}\hat\alpha _{i^-}(t)\right]\right \}
$$

其中，被控量 $u _i(t)$ 是无人机$i$ 在 t 时刻的速度(x和y方向)，$r$ 是环形编队的半径， $d = \begin{bmatrix}d _1 &d _2 &\cdots &d _N\end{bmatrix}$ 是目标角距离，满足 $\Sigma _{i=1}^Nd _i=2\pi$。$\lambda,\gamma,c _1,c _2$ 是四个正常数，需要满足 $c _1 \ge c _2$。

def circle_formation_control(radius, p_bar, p_hat, p_hat_minus, d, d_minus):
    Lambda, Gamma, C1, C2 = 1.2, 0.01, 0.4, 1.0
    p_bar = np.array(p_bar)
    p_hat = np.array(p_hat)
    p_hat_minus = np.array(p_hat_minus)
    p_bar_plus = p_bar + p_hat
    p_bar_minus = p_bar - p_hat_minus
    alpha = np.arctan2(np.cross(p_bar, p_bar_plus), np.dot(p_bar, p_bar_plus))
    if alpha < 0:
        alpha += 2*np.pi
    alpha_minus = np.arctan2(np.cross(p_bar_minus, p_bar), np.dot(p_bar_minus, p_bar))
    if alpha_minus < 0:
        alpha_minus += 2*np.pi
    l = radius**2 - np.linalg.norm(p_bar)**2
    u_p = Lambda * np.array([Gamma*l, -1, 1, Gamma*l]).reshape(2, 2) @ p_bar
    u_alpha = (d_minus * alpha - d * alpha_minus) / (d + d_minus)
    f = C1 + C2 * u_alpha / (2 * np.pi)
    u = u_p * f
    return u[0], u[1]

返回值 u 代表无人机所需的速度，再通过PID控制算法就能得出使无人机达到此速度需要的加速度值，从而给出力的信息。

launch文件

使用 python 编写 ROS2 的 launch 文件，可具有更高的灵活性。在功能包目录下新建 /launch 文件夹，并在内部创建 circle.launch.py 文件，将需要运行的进程或启动的节点写在函数 generate_launch_description 内。

启动 Gazebo

gazebo = ExecuteProcess(
    cmd=['gazebo', '-s', 'libgazebo_ros_init.so', '-s', 'libgazebo_ros_factory.so'],
    output='screen')
ld.add_action(gazebo)

启动 Gazebo 时，调用 gazebo_ros_init 插件初始化 Gazebo 和 ROS2 环境，使用 gazebo_ros_factory 插件的服务来动态生成模型。

生成无人机模型

前文提到，在无人机的描述文件 quadrotor.xacro 中定义了一个参数 namespace，用来区分不同的无人机，对该参数的赋值就是在此处进行。首先使用 xacro 包的 process_file 函数将 xacro 文件翻译成 xml 文件，同时为参数 namespace 赋值，这样每个无人机就拥有了包含自己名字空间的描述文件。接着，启动 robot_state_publisher 节点，将每个无人机的描述文件（xml 格式的字符串）实时发布出来。然后启动 spawn_entity 节点，在 Gazebo 中生成所需的无人机模型，让每个无人机订阅自己名字空间下的 /robot_description 话题，获得所需的 xml 信息。这样，就能够看到多个无人机模型在 Gazebo 仿真环境中出现了。

for i in range(num_of_quadrotors):
    doc = xacro.process_file(xacro_file, mappings={'namespace':'quad_'+str(i)})
    robot_state_publisher = Node(
        package='robot_state_publisher', executable='robot_state_publisher',
        output='screen',
        namespace='quad_'+str(i),
        parameters=[{'use_sim_time': True, 'robot_description': doc.toxml()}]
    )
    ld.add_action(robot_state_publisher)
    spawn_entity = Node(
        package='gazebo_ros', executable='spawn_entity.py',
        arguments=['-entity', 'quadrotor'+str(i),
                '-topic', 'quad_' + str(i) + '/robot_description',
                '-x', str(spawn_position[i][0]),
                '-y', str(spawn_position[i][1]),
                '-z', str(spawn_position[i][2]),
                '-Y', '0.0'],
        output='screen',
    )
    ld.add_action(spawn_entity)

启动控制代码

最后，就是启动自己编写的 python 节点，即控制所有无人机起飞和编队的节点。节点名称 circle_formation_node 是在 setup.py 文件中定义的。

circle_formation_node = Node(
    package=package_name, executable='circle_formation_node',
    output='screen',
    parameters=[{'num_of_quadrotors': num_of_quadrotors,}]
)
ld.add_action(circle_formation_node)

收尾工作

在首次编译 python 功能包前，需要对 package.xml 和 setup.py 文件进行修改。

package.xml

在编写无人机描述文件时，引入了两个插件，gazebo_ros_force 和 gazebo_ros_p3d，与它们通信使用到了两个 ROS2 话题，对应着两种特殊的消息格式，分别是 geometry_msgs 中的 Wrench 和 nav_msgs 中的 Odometry。因此，需要在 package.xml 中声明对 geometry_msgs 和 nav_msgs 的依赖，才能对功能包进行编译。

<package>
  ...
  <depend>geometry_msgs</depend>
  <depend>nav_msgs</depend>
  ...
</package>

setup.py

在 setup.py 文件中需要作两处修改。第一是在 date_files 列表中添加两个元组，将源码中的 launch 文件和 urdf(xacro) 文件复制到编译后的 /install 目录下的对应位置。

1 2	('share/' + package_name + '/launch', glob('launch/.launch.py')), ('share/' + package_name + '/urdf', glob('urdf/.*')),

第二是在 entry_points 中添加一个节点，将名为 circle_formation_node 的节点和 circle_formation.py 文件中的 main 函数建立联系。

entry_points={
    'console_scripts': [
        'circle_formation_node = quadrotor_formation.circle_formation:main',
    ],
}

GreenBlog

实现思路

创建功能包

无人机模型描述文件

无人机起飞和编队的控制代码

多线程订阅里程计话题

起飞阶段

姿态保持

编队算法

launch文件

启动 Gazebo

生成无人机模型

启动控制代码

收尾工作

package.xml

setup.py

效果展示

生成无人机模型

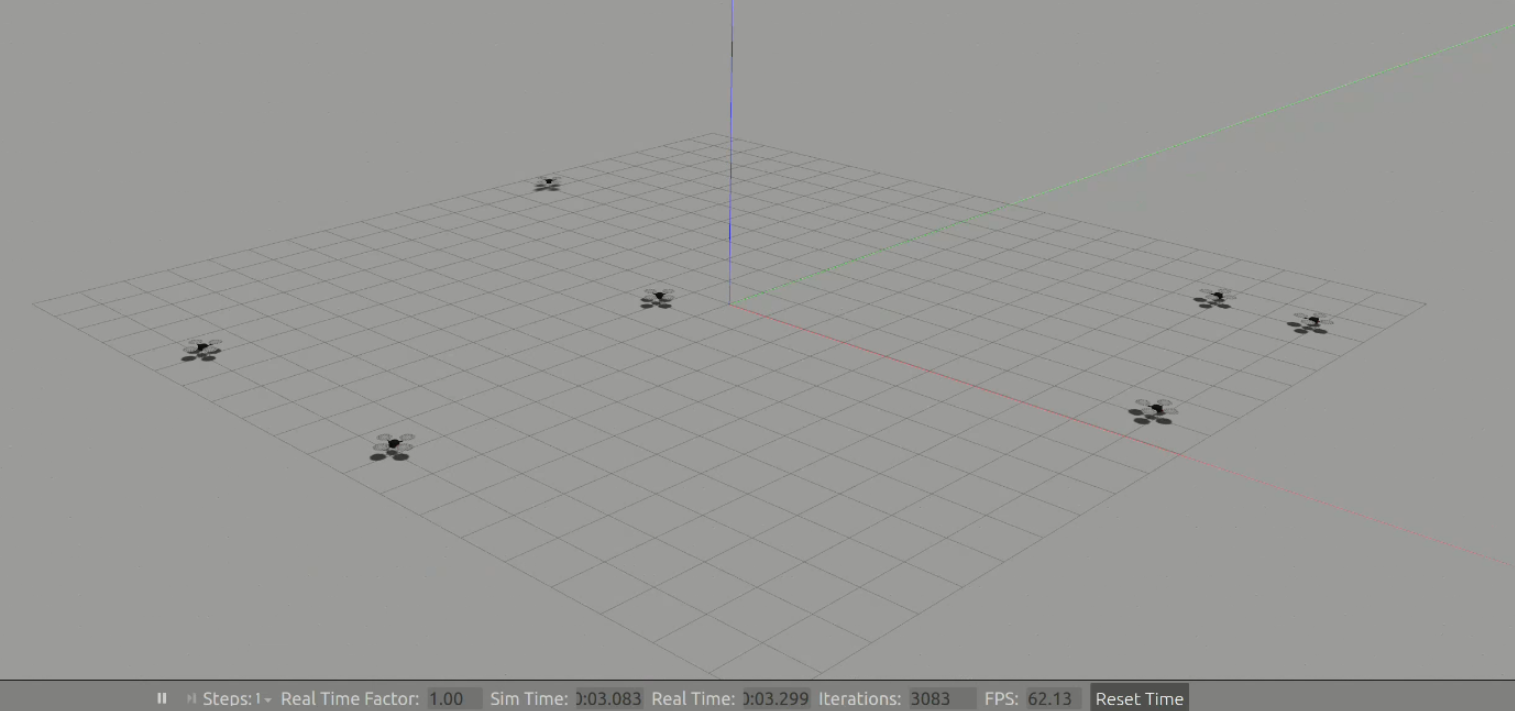
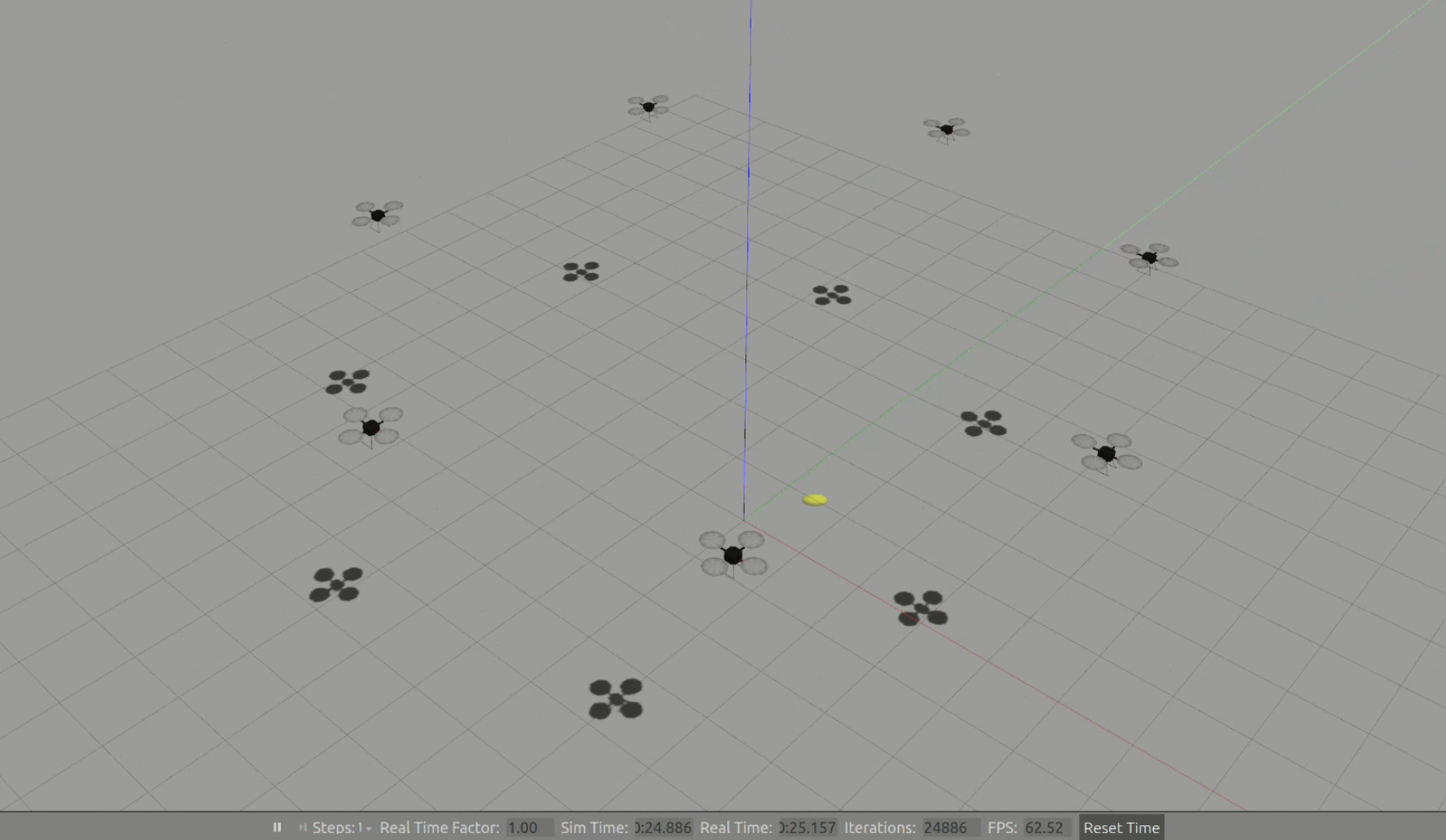
起飞到指定高度

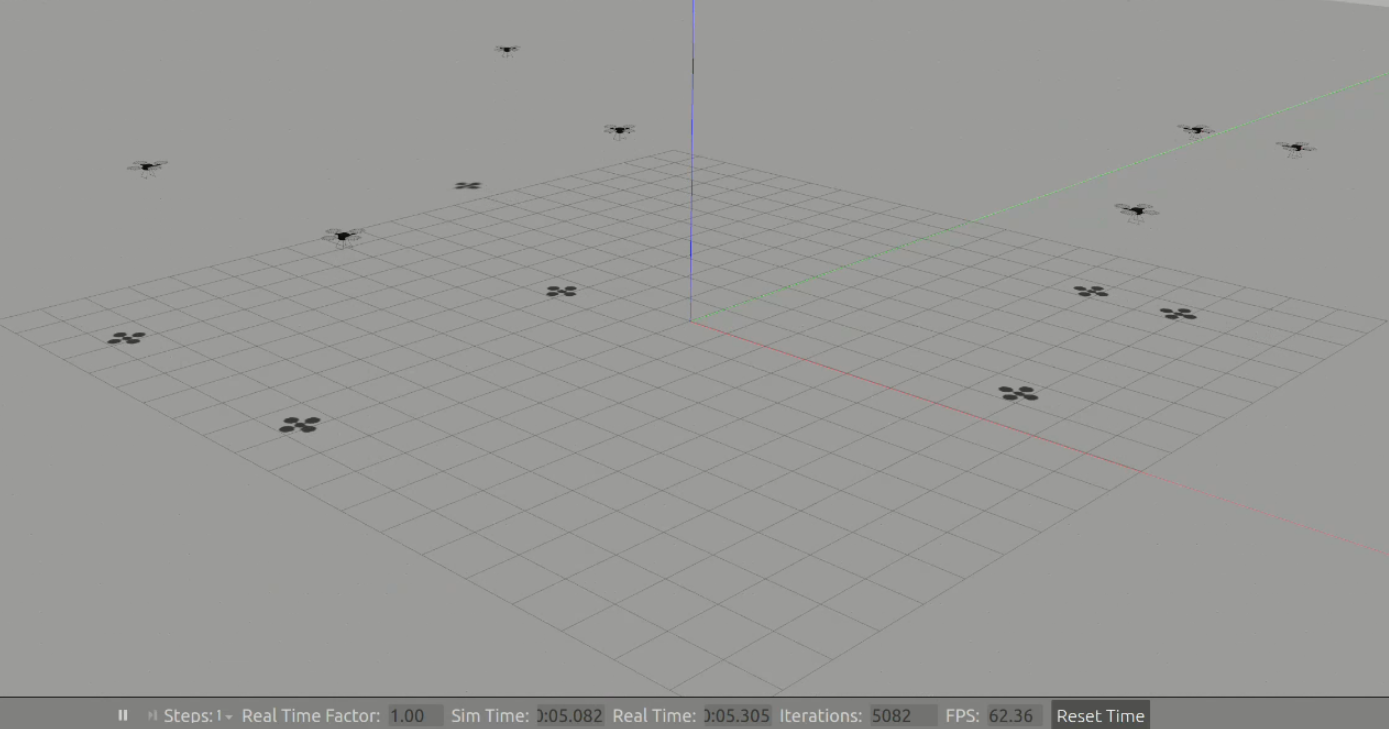
进行环形编队

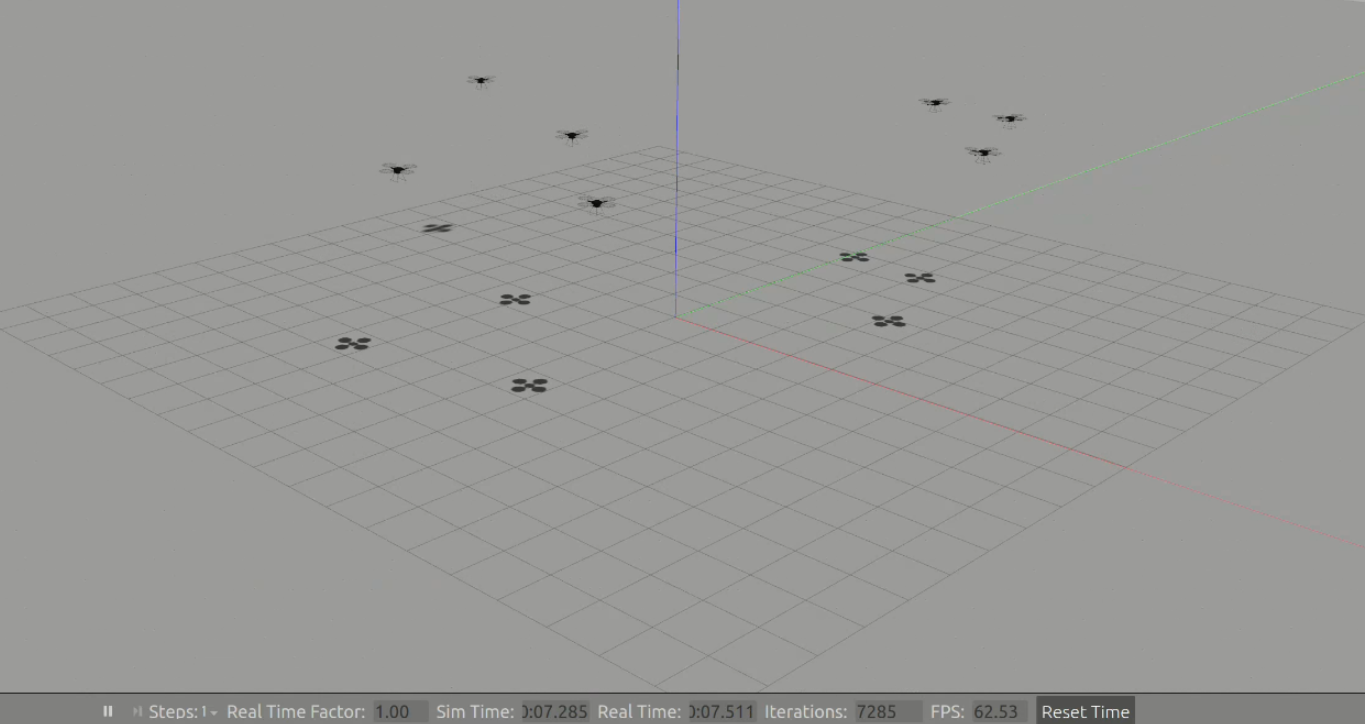
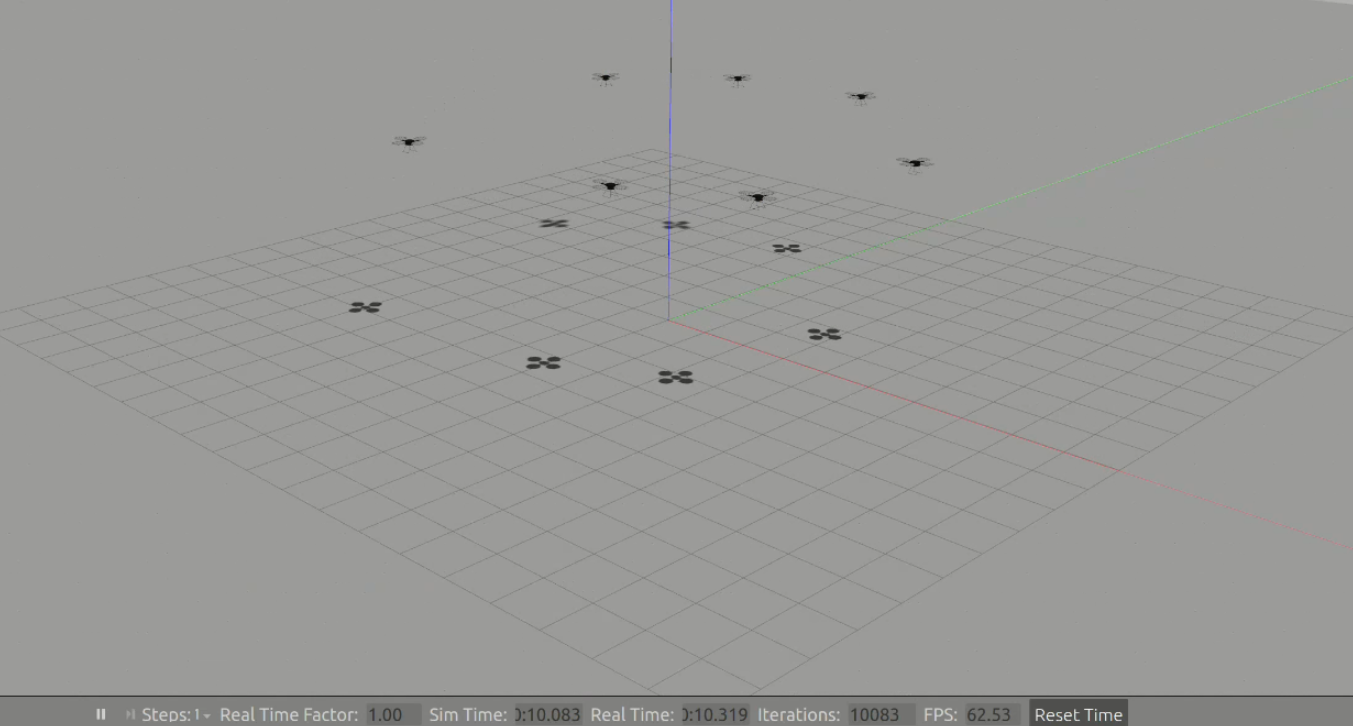
编队完成

节点关系图